Dozenal Primer Inscription

The four examples render the successor chain 1→2, 2→3, 3→4, 4→5, demonstrating that adding the simplex unit “ONE” advances X to its next value while preserving clause structure. Codes follow Kristiansen’s signary; glyph labels (“ONE”, “TWO”, …) are semantic glosses for expository clarity and do not assume phonetic values.

The Dozenal Primer Inscription is the working name for a long geometric-glyph text proposed to encode a compact dozenal (base-12) arithmetic register. The inscription is transcribed with a neutral code of sign classes (for example A01, B04, C03 and a slash-like divider P01) that mirrors the notation first used to document the shorter Scapula Glyph Inscription (KS-01). In 2024, a study argued from distributional evidence—rather than from phonetic values or a bilingual—that the text exhibits an equation-like clause structure with bound punctuation, a stereotyped medial “equals” spine, operator clusters, and a productive ×12 derivational suffix. On that account, the inscription functions as a brief primer for base-12 arithmetic, extending to compounds traditionally glossed as dozen (12×), gross (12²) and a tentative greatgross (12³).

The sign code used to publish the Dozenal Primer Inscription derives from earlier internal documentation of KS-01, which described short ruled lines, rectilinear glyphs built from a limited set of straight strokes, and visually coherent families (corners, boxes, triangles, barred posts) separated by a consistent slash divider. That memorandum cautioned that widely circulated images likely trace back to a single original drawing, and it advocated raking-light or RTI imaging before firm claims about medium, date or technique.

Overview

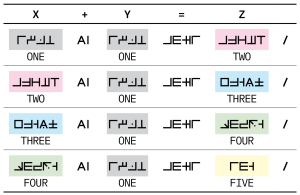
The Dozenal Primer Inscription is published only as a transcription in the Kristiansen coding scheme and as line drawings; no phonetic values or language affiliation are claimed in the 2024 analysis. Instead, the argument proceeds by methods common in Corpus linguistics and quantitative Epigraphy: (1) positional bias over initial/medial/final slots; (2) bigram inventories and pointwise mutual information to find unusually tight collocations; and (3) tests for morphological productivity at the right edge of clauses. In this model, the slash P01 behaves as bound punctuation confined to clause ends; an invariant 4-sign sequence occupies the medial spine and functions like an equals sign; a compact cluster acts as a binary addition operator; and a fixed four-sign bundle at the right edge derives “×12” forms. Complement constructions such as “11+1,” “10+2,” and “6+6” converge on the same dozen-marked targets, diagnosing 12 as the privileged base. A small number of clauses are read as scaling the same patterns to 12² and, by extension, to 12³.

The approach is intentionally agnostic about Language identification and about whether the glyphs are ultimately logographic, syllabic or something else. The claim is structural: that a small and rigid clause template—bound final punctuation, a fixed medial spine, operator clusters with narrow distribution, and a selective right-edge derivation—fits a didactic number register more parsimoniously than it fits a segmental writing system without additional evidence. Proponents note that such “equation-like” formatting is well attested in practice texts and primers across historical Numeral systems, whereas critics point out that non-linguistic genres (lists, catalogues, tallies) can sometimes mimic grammatical structure.

Glyph inventory and distribution

A compact distribution over the transcribed sign set (Kristiansen codes) is given below. Counts refer to the Dozenal Primer Inscription as published in line drawings/transcription; code labels are descriptive only and do not imply phonetic values.

Code	Glyph	Name	Freq	Init	Med	Final
A01		TRI-OPEN	5	2	3	–
A02		TRI-BAR	17	17	–	–
A03		TRI-DOT	4	–	4	–
A05		TRI-CLOSED-BAR	3	–	3	–
B01		BOX	6	4	2	–
B02		BOX-DOT	5	5	–	–
B04		BOX-DIAG-SW-NE	5	–	3	2
C01		CORNER-NW	28	14	–	14
C02		CORNER-SE	27	27	–	–
C03		CORNER-SE-DOT	6	1	5	–
C04		CORNER-NW-DIAG	3	–	3	–
C05		CORNER-SE-DIAG	16	16	–	–
C06		CORNER-NW-DIAG-DOT	7	–	7	–
H01		DOUBLE-POST-CONNECTED	15	–	15	–
H02		POST-DOUBLE-BAR	8	–	6	2
H03		DOUBLE-POST-BAR	14	–	14	–
L01		LINE-VERT	24	–	8	16
M01		COMB-2-N	20	3	16	1
M02		COMB-2-W	52	–	52	–
M03		COMB-3-E	40	–	40	–
P01		SLASH	25	–	–	25
S02		MEANDER-2-HOLLOW	9	–	3	6
S03		MEANDER-3	39	–	37	2
T01		TEE-UP	7	–	4	3
T02		TEE-LEFT	30	–	23	7
T03		UPSIDE-DOWN-TEE	38	–	19	19

Proposed numeric forms and functional sequences

Codes follow Kristiansen’s signary. Values are glosses for exposition only.. Coding scheme per Kristiansen.

Function (gloss)	Codes (Kristiansen)	Glyph sequence (icons)	Notes
ZERO	B02-M03-L01-B05-S03
ONE	C01-S03-C03-T03
TWO	C02-M02-H01-M01-T01
THREE	B01-M02-T02-A03-H02
FOUR	C05-M03-S02-C06-T02
FIVE	C01-M03-T02
SIX	C05-B04-L01
SEVEN	M01-L01-A01-T03
EIGHT	B02-M03-S03
NINE	C05-M02-H02-A05-S02
TEN	C05-M01-T02-M02-L01
ELEVEN	A01-H01-B01
TWELVE	C01-M02-H02-B04
EQUALS / clause spine	C02–M03–H03–C01		Invariant medial sequence dividing left expression from result; reported as present in every equation clause.
PLUS (binary addition)	A02–L01		High-PMI operator cluster used in successor and complement constructions.
MINUS (subtraction)	C05–M02–S02		Distinct collocational profile mirroring the syntax of the addition lines.
ONE (simplex unit)	C01–S03–C03–T03		Recurrent bundle functioning as the unit “one”; used to advance the successor chain.
PUNCTUATION (bound period)	P01 (final only)		Clause-final slash behaving as bound punctuation; not attested internally.
×12 derivation (“dozen”)	–C01–M02–H02–B04 (right edge)		Contiguous right-edge 4-gram treated as a derivational suffix forming multiples of twelve; composes with stems.

Scholarly discussion

Because the archaeological context of the longer inscription has not been publicly detailed, reception has been cautious. Supporters of the dozenal reading emphasise the conjunction of multiple independent diagnostics (final-only punctuation, a medial spine with near-zero variance, a selective right-edge four-gram, and complementary sums converging on the same target), arguing that chance alignment across all four is unlikely. Skeptics reply that without provenance, additional exemplars, or phonetic control, an arithmetic interpretation remains provisional and vulnerable to genre effects. Both sides agree on clear tests that could confirm or weaken the proposal: finding the slash P01 in non-final position; observing the putative ×12 four-gram away from clause edges; or documenting clauses that disrupt the medial spine while still behaving “arithmetically.”

Nomenclature

“Dozenal Primer Inscription” is a descriptive convenience used in secondary discussion and is not a claim about ancient self-designation. Alternative labels in circulation include “Dozenal arithmetic inscription,” “Twelve-base arithmetic inscription,” and “Kristiansen-coded arithmetic inscription.” For clarity and disambiguation within encyclopedic contexts, the present title foregrounds the proposed function (primer) and base (dozenal).

Relation to the Scapula Glyph Inscription

The Scapula Glyph Inscription (KS-01) is much shorter but provided the stable sign labels and visual classes used in the transcription of the Dozenal Primer Inscription. KS-01 shows bipartite lines and a group-final slash divider consistent with the clause architecture proposed for the longer text, although by itself the scapula piece is too brief to display a full base-12 progression. Early notes on KS-01 also highlighted the need for direct examination and higher-quality imaging before drawing conclusions about material or chronology.

See also

• Duodecimal
• Numeral system
• Mathematical notation
• Undeciphered writing systems
• Epigraphy
• Paleography